Depending on how sophisticated of a design is needed, this material can be relatively simple or full blown rocket science. So as not to scare anyone away, I'll start with the simple and easy to understand material and work on from there.

First, let's define some terms.

• Neutral Atom - This is an atom which is electrically neutral, and has the same number of protons (+1 charge) and electrons (-1 charge.) At room temperature most gases are neutral, or have bonded with other atoms to form neutral molecules. 
• Ionized Atom - An atom which receives a certain amount of energy may have one or more electrons knocked out of its orbit thus ionizing it. This results in a net positive charge on the atom. An atom that looses one electron is singly ionized, two electrons is doubly ionized, and so on.
• Ion - An ion refers to an atom or molecule which has either lost or gained an electron, and as a result is electrically charged. For the purposes of this discussion, negative ions (an extra electron) are typically not a significant contributor to the processes described here. Ions can be formed by collisions with other particles, strong electric fields, or radiation.
  
• Ionized Gas - A gas in which a significant fraction of its atoms are ionized. 
• Plasma - Plasma is a gas which is ionized to the point that it exhibits significant electrical conductivity and is characterized by high temperatures.
• Arc Discharge - This refers to an electrical current that flows through an ionized gas / plasma. The current must be large enough to self-sustain the ionized gas through which it flows. It also commonly referred to as an electrical spark.  

Let's start with something simple like an electric spark. If you take two wires and put a high enough voltage across them, a spark will jump between the two.


But how high of a voltage is required to get a spark across a certain gap? It turns out that this isn't exactly the question we should be asking, instead we need to know the electric field strength across the gap. An electric spark will occur if the electric field strength exceeds a certain value. The electric field is measured in volts per meter, and is computed by dividing the voltage across the gap by the distance of the gap. So, for a gap of 1cm with a voltage of 100V, the electric field strength is 10,000 V/m. An electric field of approximately 3,000,000 V/m is required to cause a spark, so this 100V across 1cm would not result in a spark - but 30,000 V across 1cm or 3,000V across 0.1cm would.

Now we know how to get a spark, but why is it that a spark only forms if the electric field strength is very high? Well, let's look at how an electric field effects charged particles first. It turns out that an electrically charged particle in an electric field will feel a force equal to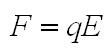


where F is the force in Newtons, q is the charge in Coulombs, and E is the electric field in volts per meter. Also, from physics we know that a force on a mass will cause an acceleration as related by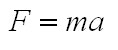

where F is the force in Newtons, m is the mass in kilograms, and a is the acceleration in meters per second per second. Accordingly, placing an electric charge in an electric field will cause a force on the charge resulting in an acceleration in the direction of the electric field. Let's imagine first an electron is placed in an electric field of varying intensity.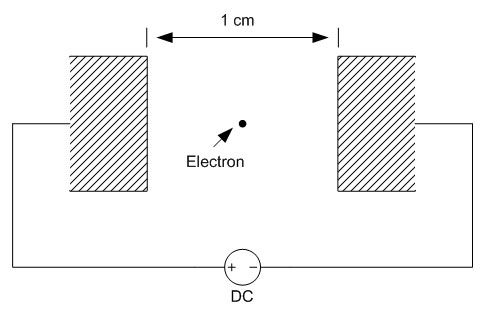

Let's start with a voltage of 0 Volts across the gap. This results in an electric field of 0 V/m, and substituting this value into equation 1 results in no force applied to the electron, and it therefor will not move. Applying a small voltage of 10mV will result in an electric field of 1 V/m. If we were to follow the substitution through equation 1 and 2 we would find that the electron accelerates at some rate towards the left. Increasing the electric field by a factor of 10 results in the electron accelerating 10 times more quickly, and so on. Keep in mind that an electron moving at a certain velocity has some kinetic energy, as given by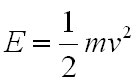

Overall, applying a stronger electric field results in any electrically charged particles in the field accelerating more quickly, and therefore possessing more kinetic energy.

Now, let's get back to how this relates to creating a spark in a gas across some gap. If we were to look at a gas on an atomic level we would see mostly neutral molecules and some few electrons. If no electric field is applied there will be no net movement of the electrons, but at very weak electric fields the electrons will begin to migrate as shown. [1]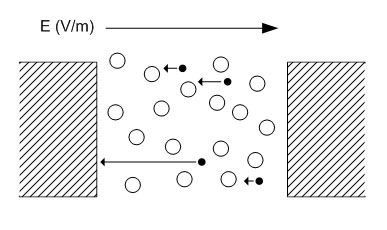

In weak electric fields (i.e. low applied voltages) only a very few electrons will make it all the way across the gap as most will collide with neutral gas molecules. Increasing the field strength will result in more free electrons making it across the gap, until at a certain voltage all of the free electrons will cross the gap. At this point, increasing the voltage further will not result in more current because all available free electrons are already crossing the gap. This sort of discharge is called the First Townsend Discharge region, and can carry only minuscule currents up to a certain saturation current value. The current characteristic for this type of discharge is shown below.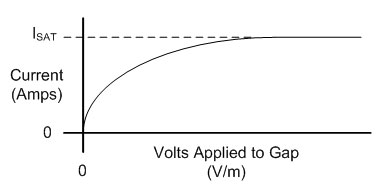

As the applied electric field is increased, the electrons will increase in speed and energy. At some point they will acquire enough energy to knock additional electrons off of neutral molecules that they collide with as they cross the gap. These additional electrons will also be accelerated across the gap and the current will begin to increase again. This sort of discharge is called the Second Townsend Discharge region, and is also limited to very small currents. [2]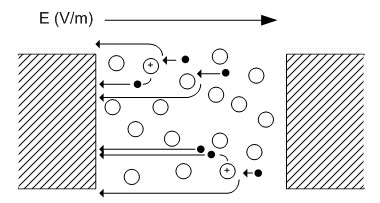

Through the Second Townsend Discharge region the positive ions created by electron collisions will move slowly in the opposite direction of the electrons toward the cathode, their lower velocity due to their higher mass. In the Second Townsend Discharge region these ions do not contribute significantly to the processes described so far. Up to this point the current that the gap can carry is a strong function of the number of naturally occurring free electrons in the gap. Since the presences of these free electrons is in no way related to the electric field, first and second Townsend discharges are essentially externally fueled and are therefore not self-sustaining.

At some higher electric field strength the positive ions flowing toward the cathode being to play a critical role. This occurs when the electric field is strong enough to give the positive ions sufficient energy that when the collide with the cathode they deposit enough energy to free electrons from the cathode surface. These free electrons are then swept towards the anode, creating electron and positive ion pairs which then repeat this process. [3]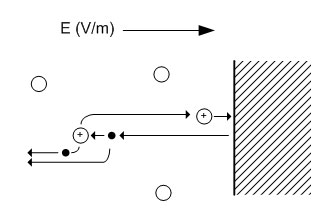

The critical process here is the creation of electrons at the cathode's surface. At some field strength this process becomes efficient enough to supply all of the electrons crossing the gap, removing any dependency on outside sources of current carriers. This is the critical point at which the discharge quickly transitions to an arc discharge, or a spark.

By observing the voltage across an arc discharge we can identify three key regions. Much of the voltage drop occurs across two invisibly thin regions directly adjoining the anode and cathode, which are referred to as the anode drop region and cathode drop region respectively. The positive column occupies the remainder of the gap. [4]


For a given current through an arc discharge, the power dissipated in the cathode drop region (arc current times cathode drop voltage) serves to heat the cathode and cause it to emit electrons, the power dissipated in the anode drop region (arc current times anode drop voltage) goes to heating the anode by electron bombardment (but serves no useful purpose), and the power dissipated in the positive column maintains the electron and ion concentrations that support the arc current.

The arc current also causes magnetic constriction of the arc column, which confines the current to a narrow cross-section. The magnetic field created by the arc current interacts with the flowing charges which creates a force that pushes inward on the arc and counteracts the tendancy of the heated gas to expand. First, let's look into how magnetic fields and moving charges interact. A simple example is a charge moving through a magnetic field which is perpendicular to the direction of motion.

Here, the charge experiences a force perpendicular to the magnetic field, and perpendicular to the direction of motion of the charge (the right hand rule is any easy way to remember this.) Next we need to establish what the magnetic field induced by the arc current looks like. In general, a straight conductor carrying a current will generate a magnetic field with lines circling the around the conductor.


This is also true when the conductor is a plasma, so if we take into account the interaction between the magnetic field and the flowing charges we can see the source of the magnetic constriction.


By looking at only a small portion of the surface of the discharge we can see that it closely resembles Fig. 8. The interaction of the magnetic field and motion of the charge results in a force on the charge towards the center of the conductor. The force is given by: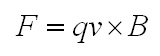


where F is the force in Newtons, q is the charge, v is the velocity of the charge, and B is the magnetic field. Note that the magnetic field B is the result of the entire current flowing through the conductor, so as the current increases so does the magnetic field strength. The stronger magnetic field in turn results in a greater compressive force which will tend to reduce the cross section through which the current flows. The smaller cross section also results in a stronger magnetic field and greater compressive force.

If these forces were the only ones at work in an arc discharge, the magnetic constriction would crush the discharge into an infinitesimally small cross section, but of course this is not the case since these compressive forces are opposed by thermal expansion from the very hot gasses in the arc discharge. In fact, increased current in an arc discharge will result in increased heat generation which will oppose the increased compressive forces. The exact dimensions of an arc discharge are therefore the result of balancing the thermal expansion due to heating, heat loss due to conduction and radiation, and the magnetic constriction resulting from the moving charges and magnetic field.

References

[1] J. D. Cobine, Gaseous Conductors, New York: McGraw-Hill Book Company, Inc., pp. 143

[2] J. D. Cobine, Gaseous Conductors, New York: McGraw-Hill Book Company, Inc., pp. 144

[3] J. D. Cobine, Gaseous Conductors, New York: McGraw-Hill Book Company, Inc., pp. 213

[4] J. D. Cobine, Gaseous Conductors, New York: McGraw-Hill Book Company, Inc., pp. 299

[ Back to Main ]

---