
Beware - we're moving in on the world of the mechanical engineer - where everything is topsy-turvy, units are imperial, and nothing is as it seems. Cv is known as the "flow coefficient", and is frequently specified for parts or equipment where it is necessary to be able to predict the rate at which fluid will flow under certain conditions. It was originally intended for liquid flows, and so it is defined as the flow rate (in gallons per minute) of water at 60 degrees Fahrenheit, across a pressure drop of 1 pound per square inch. Let's look at a more concrete example to get our heads around this. 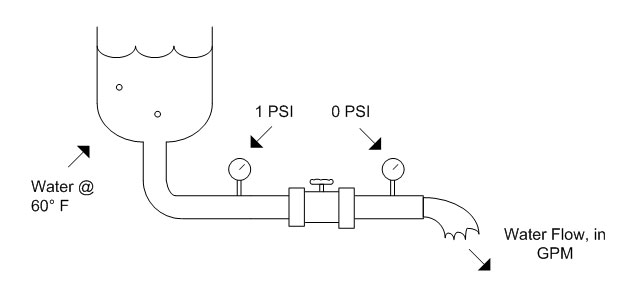 Fig. 1: Definition of Cv In the case of figure 1, if we were to measure the amount of water that flowed out of the valve in one minute, and found it to be 2 gallons, then the Cv for that valve would be 2. If we replaced the valve with perhaps a larger one and repeated this experiment and found that 10 gallons now flowed in one minute, then the Cv of that valve would be 10. From this simple experiment it is clear that the Cv value is an indication of how much flow a certain valve, constriction, tube, etc., will allow. The bigger the Cv, the higher the flow rate. Since the Cv value is calculated for water, it can't be used directly to calculate the flow of a gases. Cv does, however, give us enough information to be able to figure out the gas flow if we know a couple of things about the gas. The first thing that we need to know about the gas flow is if it is a critical flow. This has to due with the ratio of inlet to outlet pressures which is explained on the compressible flow page in the information section. If the inlet pressure is more than about twice the outlet pressure (1.89 times, to be more accurate) then the flow is said to be critical. If the flow is critical, then the flow rate is limited by a shock wave inside the valve and the flow rate is independent of the outlet pressure. If the flow is critical, the the flow rate can be calculated using this equation [1] 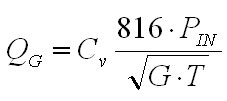 Eq. 1: Flow Rate as a Function of Cv for Critical Flows where QG is the flow rate in SCFH (standard cubic feet per hour), Cv is the flow coefficient, PIN in the inlet pressure in PSIA, G is the specific gravity of the gas, and T is the absolute temperature (° F + 460.) The specific gravity is relative to air at 70 ° F and 1 ATM, and is computed by dividing the density of the gas used by the density of air under the stated conditions. The densities of various gasses can be found on Wikipedia, among many other places. Wikipedia also has a good article on specific gravity. If the flow is not critical, then the flow rate does depend on the outlet pressure, and we need to use this equation [2] 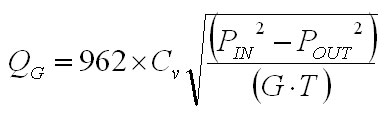 Eq. 2: Flow Rate as a Function of Cv for Sub-Critical Flows where QG is the flow rate in SCFH (standard cubic feet per hour), Cv is the flow coefficient, PIN in the inlet pressure in PSIA, POUT is the pressure at the outlet in PSIA, G is the specific gravity of the gas, and T is the absolute temperature (° F + 460.) There are other forms of these equations for fluids, and in metric. See the links at the end of this page, Especially The Engineering Toolbox. References [1] Ideal Valve Inc., "Flow Calculations for Needle Valves", August 2007, http://www.idealvalve.com/flowcal.htm [2] Ideal Valve Inc., "Flow Calculations for Needle Valves", August 2007, http://www.idealvalve.com/flowcal.htm Links The Engineering Toolbox, Control Valves Ideal Valve Inc., Flow Calculations For Needle Valves Prof. Michael L. Corradini, Department of Engineering Physics, University of Wisconsin, Fundamentals of Multiphase Flow [ Back to Main ] Questions?
Comments? Suggestions? E-Mail me at MyElectricEngine@gmail.com
Copyright 2007-2010 by Matthew Krolak - All Rights Reserved. Don't copy my stuff without asking first. |